Questions about synthetic control methods in causal inference

Andy Wheeler writes:

I think this back and forth may be of interest to you and your readers.

There was a published paper attributing very large increases in homicides in Philadelphia to the policies by progressive prosecutor Larry Krasner (+70 homicides a year!). A group of researchers then published a thorough critique, going through different potential variants of data and models, showing that quite a few reasonable variants estimate reduced homicides (with standard errors often covering 0):

– Hogan original paper,
– Kaplan et al critique
– Hogan response
– my writeup

I know those posts are a lot of weeds to dig into, but they touch on quite a few topics that are recurring themes for your blog—many researcher degrees of freedom in synthetic control designs, published papers getting more deference (the Kaplan critique was rejected by the same journal), a researcher not sharing data/code and using that obfuscation as a shield in response to critics (e.g. your replication data is bad so your critique is invalid).

I took a look, and . . . I think this use of synthetic control analysis is not good. I pretty much agree with Wheeler, except that I’d go further than he does in my criticism. He says the synthetic control analysis in the study in question has data issues and problems with forking paths; I’d say that even without any issues of data and forking paths (for example, had the analysis been preregistered), I still would not like it.

Overview

Before getting to the statistical details, let’s review the substantive context. From the original article by Hogan:

De-prosecution is a policy not to prosecute certain criminal offenses, regardless of whether the crimes were committed. The research question here is whether the application of a de-prosecution policy has an effect on the number of homicides for large cities in the United States. Philadelphia presents a natural experiment to examine this question. During 2010–2014, the Philadelphia District Attorney’s Office maintained a consistent and robust number of prosecutions and sentencings. During 2015–2019, the office engaged in a systematic policy of de-prosecution for both felony and misdemeanor cases. . . . Philadelphia experienced a concurrent and historically large increase in homicides.

I would phrase this slightly differently. Rather than saying, “Here’s a general research question, and we have a natural experiment to learn about it,” I’d prefer the formulation, “Here’s something interesting that happened, and let’s try to understand it.”

It’s tricky. On one hand, yes, one of the major reasons for arguing about the effect of Philadelphia’s policy on Philadelphia is to get a sense of the effect of similar policies there and elsewhere in the future. On the other hand, Hogan’s paper is very much focused on Philadelphia between 2015 and 2019. It’s not constructed as an observational study of any general question about policies. Yes, he pulls out some other cities that he characterizes as having different general policies, but there’s no attempt to fully involve those other cities in the analysis; they’re just used as comparisons to Philadelphia. So ultimately it’s an N=1 analysis—a quantitative case study—and I think the title of the paper should respect that.

Following our “Why ask why” framework, the Philadelphia story is an interesting data point motivating a more systematic study of the effect of prosecution policies and crime. For now we have this comparison of the treatment case of Philadelphia to the control of 100 other U.S. cities.

Here are some of the data. From Wheeler (2023), here’s a comparison of trends in homicide rates in Philadelphia to three other cities:

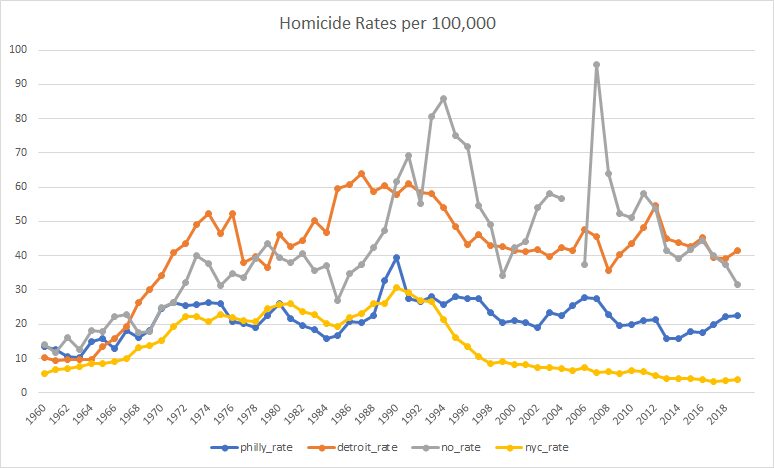
Wheeler chooses these particular three comparison cities because they were the ones that were picked by the algorithm used by Hogan (2022). Hogan’s analysis compares Philadelphia from 2015-2019 to a weighted average of Detroit, New Orleans, and New York during those years, with those cities chosen because their weighted average lined up to that of Philadelphia during the years 2010-2014. From Hogan:

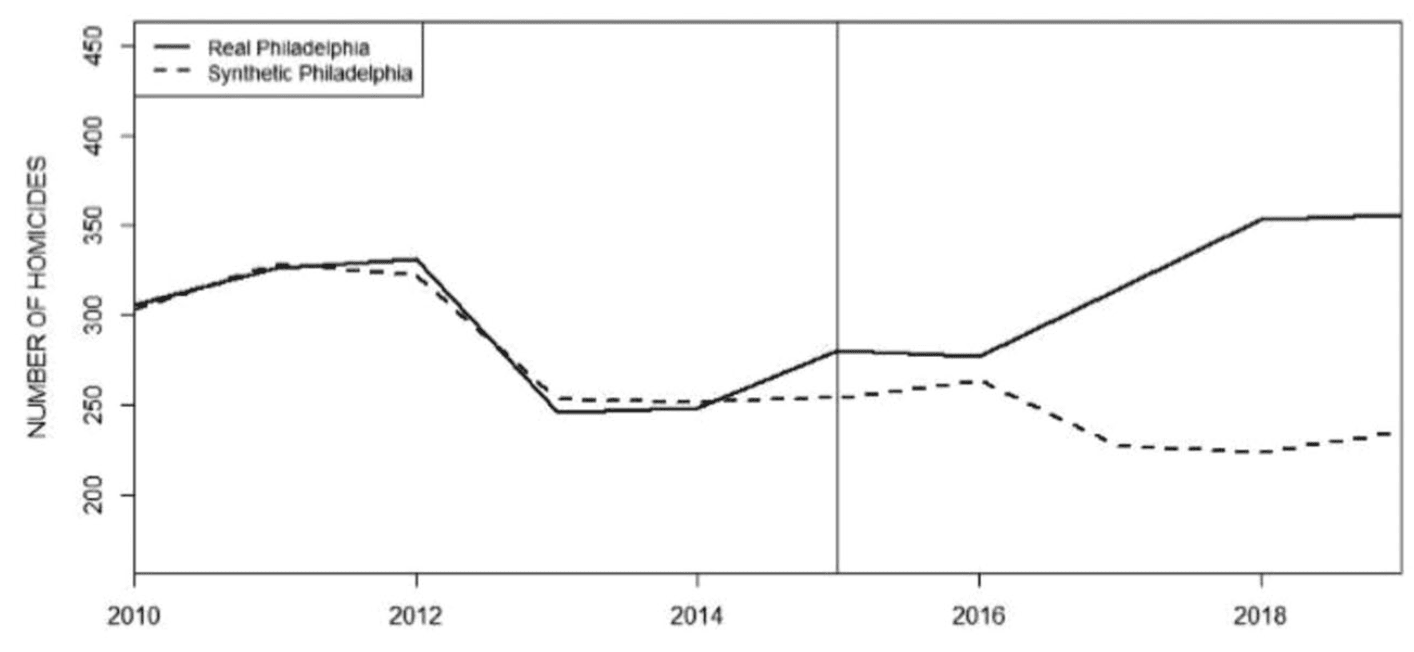
As Wheeler says, it’s kinda goofy for Hogan to line these up using homicide count rather than homicide rates . . . I’ll have more to say in a bit regarding this use of synthetic control analysis. For now, let me just note that the general pattern in Wheeler’s longer time series graph is consistent with Hogan’s story: Philadelphia’s homicide rate moved up and down over the decades, in vaguely similar ways to the other cities (increasing throughout the 1960s, slightly declining in the mid-1970s, rising again in the late-1980s, then gradually declining since 1990), but then steadily increasing from 2014 onward. I’d like to see more cities on this graph (natural comparisons to Philadelphia would be other Rust Belt cities such as Baltimore and Cleveland. Also, hey, why not show a mix of other large cities such as LA, Chicago, Houston, Miami, etc.) but this is what I’ve got here. Also it’s annoying that the above graphs stop in 2019. Hogan does have this graph just for Philadelphia that goes to 2021, though:

As you can see, the increase in homicides in Philadelphia continued, which is again consistent with Hogan’s story. Why only use data up to 2019 in the analyses? Hogan writes:

The years 2020–2021 have been intentionally excluded from the analysis for two reasons. First, the AOPC and Sentencing Commission data for 2020 and 2021 were not yet available as of the writing of this article. Second, the 2020–2021 data may be viewed as aberrational because of the coronavirus pandemic and civil unrest related to the murder of George Floyd in Minnesota.

I’d still like to see the analysis including 2020 and 2021. The main analysis is the comparison of time series of homicide rates, and, for that, the AOPC and Sentencing Commission data would not be needed, right?

In any case, based on the graphs above, my overview is that, yeah, homicides went up a lot in Philadelphia since 2014, an increase that coincided with reduced prosecutions and which didn’t seem to be happening in other cities during this period. At least, so I think. I’d like to see the time series for the rates in the other 96 cities in the data as well, going from, say, 2000, all the way to 2021 (or to 2022 if homicide data from that year are now available).

I don’t have those 96 cities, but I did find this graph going up to 2000 from a different Wheeler post:

Ignore the shaded intervals; what I care about here is the data. (And, yeah, the graph should include zero, since it’s in the neighborhood.) There has been a national increase in homicides since 2014. Unfortunately, from this national trend line alone I can’t separate out Philadelphia and any other cities that might have instituted a de-prosecution strategy during this period.

So, my summary, based on reading all the articles and discussions linked above, is . . . I just can’t say! Philadelphia’s homicide rate went up since 2014 during the same period that it decreased prosecutions, and this was part of a national trend of increased homicides—but there’s no easy way given the directly available information to compare to other cities with and without that policy. This is not to say that Hogan is wrong about the policy impacts, just that I don’t see any clear comparisons here.

The synthetic controls analysis

Hogan and the others make comparisons, but the comparisons they make are to that weighted average of Detroit, New Orleans, and New York. The trouble is . . . that’s just 3 cities, and homicide rates can vary a lot from city to city. It just doesn’t make sense to throw away the other 96 cities in your data. The implied counterfactual is that if Philadelphia had continued post-2014 with its earlier sentencing policy, that its homicide rates would look like this weighted average of Detroit, New Orleans, and New York—but there’s no reason to expect that, as this averaging is chosen by lining up the homicide rates from 2010-2014 (actually the counts and populations, not the rates, but that doesn’t affect my general point so I’ll just talk about rates right now, as that’s what makes more sense).

And here’s the point: There’s no good reason to think that an average of three cities that give you numbers comparable to Philadelphia’s for the homicide rates in the five previous years will give you a reasonable counterfactual for trends in the next five years. To think there’s no mathematical reason we should expect the time series to work that way, nor do I see any substantive reason based on sociology or criminology or whatever to expect anything special from a weighted average of cities that is constructed to line up with Philadelphia’s numbers for those three years.

The other thing is that this weighted-average thing is not what I’d imagined when I first heard that this was a synthetic controls analysis.

My understanding of a synthetic controls analysis went like this. You want to compare Philadelphia to other cities, but there are no other cities that are just like Philadelphia, so you break up the city into neighborhoods and find comparable neighborhoods in other cities . . . and when you’re done you’ve created this composite “city,” using pieces of other cities, that functions as a pseudo-Philadelphia. In creating this composite, you use lots of neighborhood characteristics, not just matching on a single outcome variable. And then you do all of this with other cities in your treatment group (cities that followed a de-prosecution strategy).

The synthetic controls analysis here differed from what I was expecting in three ways:

1. It did not break up Philadelphia and the other cities into pieces, jigsaw-style. Instead, it formed a pseudo-Philadelphia by taking a weighted average of other cities. This is a much more limited approach, using much less information, and I don’t see it as creating a pseudo-Philadelphia in the full synthetic-controls sense.

2. It only used that one variable to match the cities, leading to concerns about comparability that Wheeler discusses.

3. It was only done for Philadelphia; that’s the N=1 problem.

Researcher degrees of freedom, forking paths, and how to think about them here

Wheeler points out many forking paths in Hogan’s analysis, lots of data-dependent decision rules in the coding and analysis. (One thing that’s come up before in other settings: At this point, you might ask how do we know that Hogan’s decisions were data-dependent, as this is a counterfactual statement involving the analyses he would’ve had done had the data been different. And my answer, as in previous cases, is that, given that the analysis was not pre-registered, we can only assume it is data-dependent. I say this partly because every non-preregistered analysis I’ve ever done has been in the context of the data, also because if all the data coding and analysis decisions had been made ahead of time (which is what been required for these decisions to not be data-dependent), then why not preregister? Finally let me emphasize that researcher degrees of freedom and forking paths do not represent criticisms of flaws of a study; they’re just a description of what was done, and in general I don’t think they’re a bad thing at all; indeed, almost all the papers I’ve ever published include many many data-dependent coding and decision rules.)

Given all the forking paths, we should not take Hogan’s claims of statistical significance at face value, and indeed the critics find that various alternative analyses can change the results.

In their criticism, Kaplan et al. say that reasonable alternative specifications can lead to null or even opposite results compared to what Hogan reported. I don’t know if I completely buy this—given that Philadelphia’s homicide rate increased so much since 2014, it seems hard for me to see how a reasonable estimate would find that its policy rate reduced the homicide rate.

To me, the real concern is with comparing Philadelphia to just three other cities. Forking paths are real, but I’d have this concern even if the analysis were identical and it had been preregistered. Preregister it, whatever, you’re still only comparing to three cities, and I’d like to see more.

Not junk science, just difficult science

As Wheeler implicitly says in his discussion, Hogan’s paper is not junk science—it’s not like those papers on beauty and sex ratio, or ovulation and voting, or air rage, himmicanes, ages ending in 9, or the rest of our gallery of wasted effort. Hogan and the others are studying real issues. The problem is that the data are observational, the data are sparse and highly variable; that is, the problem is hard. And it doesn’t help when researchers are under the impression that these real difficulties can be easily resolved using canned statistical identification techniques. In that aspect, we can draw an analogy to the notorious air-pollution-in-China paper. But this one’s even harder, in the following sense: The air-pollution-in-China paper included a graph with two screaming problems: an estimated life expectancy of 91 and an out-of-control nonlinear fitted curve. In contrast, the graphs in the Philadelphia-analysis paper all look reasonable enough. There’s nothing obviously wrong with the analysis, and the problem is a more subtle issue of the analysis not fully accounting for variation in the data.

from Hacker News https://ift.tt/XeBPTcw