In this series we explore the wonderful world of the bounding volume hierarchy: the mysterious data structure that enables real-time ray tracing on recent GPUs, in complex, animated scenes. Despite the broad adoption of ray tracing in games, in-depth understanding of the underlying technology seems to be reserved to a select few. In this article we show how a proper BVH is implemented without support from DXR / RTX / OptiX / Vulkan, in easy-to-read ‘sane C++’. Whether this is actually useful for you, or just interesting as background information, depends on your needs, obviously.
This series will grow in a few stages. The final version will consist of five articles:
- Basics: data structure, simple construction and ray traversal (this article).
- Faster rays: the Surface Area Heuristic and ordered traversal.
- Faster construction: binned BVH building.
- BVHs for animated scenes: refitting, rebuilding and top-level BVHs.
- Even faster rays: spatial splits and tree rotations.
In this first article we discuss the bare basics: what the BVH is used for, and how a basic BVH is constructed and traversed with a ray. The end product is a simple but reasonably efficient CPU ray tracer, which we will further improve upon in subsequent articles.
Background
The BVH is an acceleration structure. It serves to reduce a pretty fundamental problem in ray tracing: the sheer cost of finding the nearest intersection of a ray and a scene consisting of (potentially) millions of polygons. The basic principle is easy to understand: if we have 64 polygons, we could split them into two groups of 32 polygons, each group enclosed by a bounding volume such as a box or a sphere. When intersecting the scene, we can skip 32 polygons if the ray does not intersect the enclosing volume, nearly halving the processing time. Next, we do the same to each of the two groups: split in two halves, encapsulate, recurse. The resulting bounding volume hierarchy brings down processing time to manageable levels: with each level, we halve the number of polygons. Starting with 64 polygons, we traverse a tree in six steps to arrive at a single polygon.
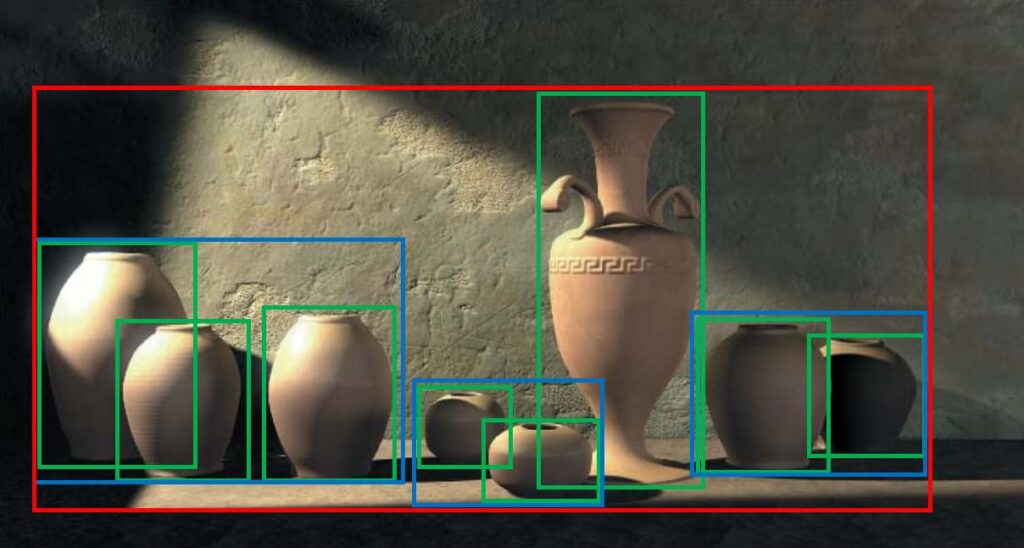
That’s the global idea, but let’s make things practical. I will be using a minimalistic template from one of my courses for these experiments, but the code is designed to be generic. Feel free to use something else.
We start with the definition of a triangle:
struct Tri { float3 vertex0, vertex1, vertex2; float3 centroid; };
Your triangle may need more properties for rendering, but for building a BVH and intersecting the triangle with a ray, this is all we need. Speaking of rays:
struct Ray { float3 O, D; float t = 1e30f; };Here, O is the ray origin, D is the (typically normalized) ray direction. Scalar t is the distance at which we found an intersection, which gets initialized to ‘infinity’ (well, almost) here.
Let’s construct some random triangles to play with:
// triangle count
#define N 64
Tri tri[N];
// application init; gets called once at startup
void BasicBVHApp::Init()
{
for (int i = 0; i < N; i++)
{
float3 r0( RandomFloat(), RandomFloat(), RandomFloat() );
float3 r1( RandomFloat(), RandomFloat(), RandomFloat() );
float3 r2( RandomFloat(), RandomFloat(), RandomFloat() );
tri[i].vertex0 = r0 * 9 - float3( 5 );
tri[i].vertex1 = tri[i].vertex0 + r1;
tri[i].vertex2 = tri[i].vertex0 + r2;
}
}Here, RandomFloat() yields a uniform random number in the range 0..1. I used Marsaglia’s Xor32 RNG, but anything will do. Given three vectors with random components, a triangle is then produced within a 10x10x10 cube centered around the origin. Not pretty, but good enough for now. Feel free to replace this with a proper model, e.g. imported using assimp or TinyOBJ.
Next, we need a way to intersect a triangle with a ray:
void IntersectTri( Ray& ray, const Tri& tri )
{
const float3 edge1 = tri.vertex1 - tri.vertex0;
const float3 edge2 = tri.vertex2 - tri.vertex0;
const float3 h = cross( ray.D, edge2 );
const float a = dot( edge1, h );
if (a > -0.0001f && a < 0.0001f) return; // ray parallel to triangle
const float f = 1 / a;
const float3 s = ray.O - tri.vertex0;
const float u = f * dot( s, h );
if (u < 0 || u > 1) return;
const float3 q = cross( s, edge1 );
const float v = f * dot( ray.D, q );
if (v < 0 || u + v > 1) return;
const float t = f * dot( edge2, q );
if (t > 0.0001f) ray.t = min( ray.t, t );
}This is the famous Möller–Trumbore intersection algorithm, which is still pretty close to ‘as fast as possible’. There exist slightly faster approaches (see Chapter 5 of Sven’s thesis), but these need more (or rather, different) data than just the three vertices.
The IntersectTri function determines if there is an intersection between the ray and the triangle. If this is the case, we check if the found intersection distance is closer than what the ray encountered before. If so, the t value for the ray is updated. For a given ray, we can now simply check all triangles; after doing so, the ray ‘knows’ the shortest distance to a surface in the scene.
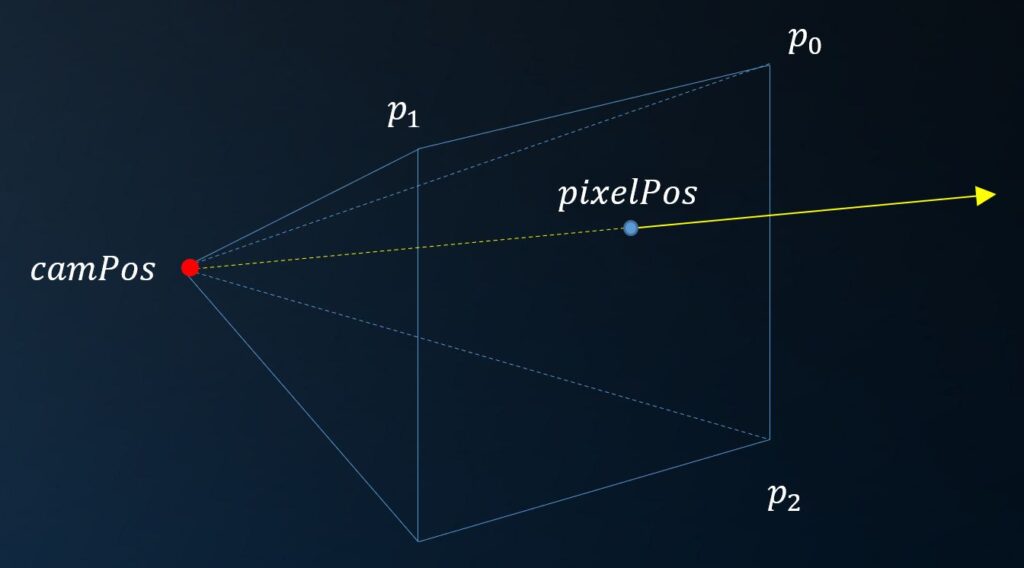
So, let’s generate some rays. For e.g. a 640 x 640 image, we do this by firing rays from a camera position to a virtual screen plane:
float3 camPos( 0, 0, -18 );
float3 p0( -1, 1, -15 ), p1( 1, 1, -15 ), p2( -1, -1, -15 );
Ray ray;
for (int y = 0; y < 640; y++) for (int x = 0; x < 640; x++)
{
float3 pixelPos = p0 + (p1 - p0) * (x / 640.0f) + (p2 - p0) * (y / 640.0f);
ray.O = camPos;
ray.D = normalize( pixelPos - ray.O );
ray.t = 1e30f;Here, the camera is placed at position (0,0,-18), so: well outside the cube that contains the triangles. Virtual screen corners are located at (-1, 1, -15), (1,1,-15) and (-1,-1,-15), so 3 units in front of the camera. For each of the pixels we can now calculate a position on this square. The ray is then initialized with the camera position as origin, and a normalized vector from the ray origin to the pixel position as a direction.
With a properly initialized primary ray we can now get our first ray traced view of the test scene, by ‘brute force’ checking the ray against every triangle. The result is a t value in the ray for each pixel. This value is 1e30f if we hit nothing, or the actual distance to a triangle otherwise.
for( int i = 0; i < N; i++ ) IntersectTri( ray, tri[i] );
The result is underwhelming, but hey, it shows that the basic setup works. I’ll leave the explanation of proper Whitted-style ray tracing to Peter Shirley‘s amazing book and focus on the efficiency of those rays instead.
Concepts and Ingredients
On my machine, it takes about 140 milliseconds to construct the 640 x 640 rays and intersect them with the 64 triangles. That’s not bad by the way: we trace almost 3 million rays per second, and that’s not even using multithreading or the GPU. Thing is, however: computation scales linearly in the number of triangles… Tracing 256 triangles takes 540 milliseconds; 1024 triangles bring this to 2250 milliseconds.
Time to introduce the BVH.
When Rubin & Whitted first described the bounding volume hierarchy, they assumed the bounding volumes would be placed manually. This is not something artists will enjoy, so let’s see how a BVH can be constructed automatically.
We start with the scene and it’s bounding box. This is going to be the root node for the hierarchy. We then recursively subdivide this node. A split plane partitions the primitives in two sets. Note that we do not split space: this might lead to primitives being split and/or assigned to both sides. In a BVH this never happens. The partitioning is what we need the primitive centroids for: each triangle (or disc, in the figure above) is either to the left of the split plane, or not to the left (which includes the situation where the primitive is on the split plane – we need to be precise!).
After the split we have two (now independent) groups of objects, with their updated group bounds:
Note that the bounding volumes of the two groups may overlap. This actually happens when we split the right group vertically:
Splitting the left group also leads to an interesting situation: the group of discs at the top and the single disc at the bottom have bounds that are pretty far apart. A ray that does intersect the left group may thus miss both of its child nodes, avoiding intersection tests with seven discs.
For a BVH node we need the following data:
- The bounds. In our case: an axis-aligned bounding box (AABB), which is easy to calculate and cheap to store: just 6 floats define the AABB in 3D space. Note: a sphere would be even cheaper to store, but it is not as convenient to work with in practice.
- References to the two child nodes, if the node is not a leaf node.
- References to primitives, if the node is a leaf node.
A naïve BVH node layout would look something like:
struct BVHNode
{
aabb nodeBounds;
BVHNode* left, *right;
bool isLeaf;
vector<Tri*> primitives;
};However, this struct has many problems. It’s rather large, but also somewhat unpredictable in size due to the vector and the pointers, which take up 4 bytes on a 32-bit OS, but 8 on a 64-bit OS.
The first improvement is switching from pointers to indices. For triangles we use their indices in the triangle array; for child node pointers we can do something similar if we pre-allocate all nodes that we ever need in a BVHNode pool. We can do this, because the size of the BVH for N triangles has an upper limit: we can never have more than 2N-1 nodes, since N primitives in N leafs have no more than N/2 parents, N/4 grandparents and so on.
With primitive pointers and BVHNode pointers replaced by indices the BVHNode struct reduces to:
struct
{
float3 aabbMin, aabbMax; // 24 bytes
uint leftChild, rightChild; // 8 bytes
bool isLeaf; // 4 bytes
uint firstPrim, primCount; // 8 bytes; total: 44 bytes
}; Note how we cleverly store a list of primitives using just two numbers: we simply store the index of the first primitive, and the number of primitives. This way, any number of primitives can be specified in just eight bytes, as long as they are stored consecutively in the primitive array. It turns out that we can enforce this elegantly.
We can make several improvements; most of these I will mention later but one is useful now: boolean isLeaf is redundant once we realize that for a leaf the primCount cannot be zero, while for all other nodes leftChild and rightChild cannot be zero. This yields (for now) the final structure with a size of 40 bytes.
Construction
We can now start the actual construction of the hierarchy. The first step is the creation of the root node, which we will then recursively subdivide.
BVHNode bvhNode[N * 2 - 1];
uint rootNodeIdx = 0, nodesUsed = 1;
void BuildBVH()
{
for (int i = 0; i < N; i++) tri[i].centroid =
(tri[i].vertex0 + tri[i].vertex1 + tri[i].vertex2) * 0.3333f;
// assign all triangles to root node
BVHNode& root = bvhNode[rootNodeIdx];
root.leftChild = root.rightChild = 0;
root.firstPrim = 0, root.primCount = N;
UpdateNodeBounds( rootNodeIdx );
// subdivide recursively
Subdivide( rootNodeIdx );
}The first lines of this function initialize the centroids for the triangles, which are needed for the subdivision process. After that, we claim one node from the bvhNode array. The root node is initialized: the child references are zeroed, and all primitives are added to it.
Updating the AABB for the root node is straightforward:
void UpdateNodeBounds( uint nodeIdx )
{
BVHNode& node = bvhNode[nodeIdx];
node.aabbMin = float3( 1e30f );
node.aabbMax = float3( -1e30f );
for (uint first = node.firstPrim, i = 0; i < node.primCount; i++)
{
Tri& leafTri = tri[first + i];
node.aabbMin = fminf( node.aabbMin, leafTri.vertex0 );
node.aabbMin = fminf( node.aabbMin, leafTri.vertex1 );
node.aabbMin = fminf( node.aabbMin, leafTri.vertex2 );
node.aabbMax = fmaxf( node.aabbMax, leafTri.vertex0 );
node.aabbMax = fmaxf( node.aabbMax, leafTri.vertex1 );
node.aabbMax = fmaxf( node.aabbMax, leafTri.vertex2 );
}
}Note: The fminf and fmaxf functions used here return the minimum and maximum x, y and z for pairs of float3‘s. Each vertex of each triangle in the BVHNode is visited to find the lowest and highest x, y and z: the resulting set of six values is the AABB we are looking for.
Finally, we recursively subdivide the root node. A few steps are required:
- Determine the axis and position of the split plane
- Split the group of primitives in two halves using the split plane
- Create child nodes for each half
- Recurse into each of the child nodes.
1. Split plane axis and position: for now, we will split the AABB along its longest axis. Later we will discuss better ways, but for now this is fine. Code:
float3 extent = node.aabbMax - node.aabbMin;
int axis = 0;
if (extent.y > extent.x) axis = 1;
if (extent.z > extent[axis]) axis = 2;
float splitPos = node.aabbMin[axis] + extent[axis] * 0.5f;2. Split the group in two halves: this sounds like a complicated thing to do, but in BVH construction this is surprisingly simple. Because we are not splitting any triangles, the combined size of the list of triangles in both halves is exactly the size of the unsplit list. That means the split can be done in place. For this, we walk the list of primitives, and swap each primitive that is not on the left of the plane with a primitive at the end of the list. This is functionally equivalent to a QuickSort partition.
int i = node.firstPrim;
int j = i + node.primCount - 1;
while (i <= j)
{
if (tri[i].centroid[axis] < splitPos)
i++;
else
swap( tri[i], tri[j--] );
}Note that the triangles do not need to be sorted; it is sufficient that the two groups of triangles on both sides of the split plane are stored consecutively.
3. Creating child nodes for each half: Using the outcome of the partition loop we construct two child nodes. The first child node contains the primitives at the start of the array; the second child node contains the primitives starting at i. The number of primitives on the left is thus i - node.firstPrim; the right child has the remaining primitives. In code:
int leftCount = i - node.firstPrim;
if (leftCount == 0 || leftCount == node.primCount) return;
// create child nodes
int leftChildIdx = nodesUsed++;
int rightChildIdx = nodesUsed++;
node.leftNode = leftChildIdx;
bvhNode[leftChildIdx].firstPrim = node.firstPrim;
bvhNode[leftChildIdx].primCount = leftCount;
bvhNode[rightChildIdx].firstPrim = i;
bvhNode[rightChildIdx].primCount = node.primCount - leftCount;
node.primCount = 0;Some details to point out here:
- Theoretically, the split in the middle can yield an empty box on the left or the right side. Not easy to come up with such a situation though! Left as an exercise for the reader. 😉
- We should not forget to set the primitive count of the node we just split to zero. Since we do not store the
isLeafboolean anymore, we rely on theprimCountto identify leafs and interior nodes. - Since we increment the ‘next free bvh node counter’
nodesUsedtwice on consecutive lines, it is obvious thatrightChildIdxis always equal toleftChildIdx + 1. This of course should have consequences for theBVHNodestruct, which gets reduced to 36 bytes.
We’re almost done with the subdivide functionality. One we have generated the left and right child nodes, we update their bounds (using a call to UpdateNodeBounds, which we created earlier), and we recurse into the child nodes (using a call to the Subdivide function we’re currently writing). Leaves us with one question: when does the recursion end? One would say: once there is one primitive left. This is sadly not true. The point is, two triangles quite often form a quad in real-world scenes. If this quad is axis-aligned, there is no way we can split it (with an axis-aligned plane) into two non-empty halves. For this reason, we typically terminate when we have 2 or less primitives in a leaf. Even this is not completely safe – but for a solution we need a seemingly unrelated technique, which will be discussed in the next article.
One More Thing
There is one nagging oversight in the partition code that we need to fix. I am talking about this line:
swap( tri[i], tri[j--] );This line has two issues. First, we are changing the original list of triangles. This may be fine if it is owned by the BVH builder, but not so great if it is shared with e.g. the animation system of an engine. Secondly, we are swapping whole triangles by value. Their size is somewhat limited in this case, but what if a triangle has uv-coordinates, material ids, a name and so on?
We can resolve these issues by using an intermediate array with triangle indices. It contains simple unsigned integers and gets initialized with the numbers 0..N-1. From then on, we swap entries in this array, rather than the triangles themselves. A BVHNode leaf now references a slice of indices, rather than a set of consecutive triangles. It’s an extra step of indirection, but it proves to be quite practical.
We make a few small changes to facilitate this new data structure:
Tri tri[N];
uint triIdx[N];
At the start of BuildBVH we initialize this array:
void BuildBVH()
{
// populate triangle index array
for (int i = 0; i < N; i++) triIdx[i] = i;
....The BVHNode struct needs some updates to member variable names, and now also incorporates some of the other changes we discussed:
struct BVHNode
{
float3 aabbMin, aabbMax;
uint leftNode, firstTriIdx, triCount;
bool isLeaf() { return triCount > 0; }
};UpdateBounds now uses the new indirection:
void UpdateNodeBounds( uint nodeIdx )
{
BVHNode& node = bvhNode[nodeIdx];
node.aabbMin = float3( 1e30f );
node.aabbMax = float3( -1e30f );
for (uint first = node.firstTriIdx, i = 0; i < node.triCount; i++)
{
uint leafTriIdx = triIdx[first + i];
Tri& leafTri = tri[leafTriIdx];
node.aabbMin = fminf( node.aabbMin, leafTri.vertex0 ),
node.aabbMin = fminf( node.aabbMin, leafTri.vertex1 ),
node.aabbMin = fminf( node.aabbMin, leafTri.vertex2 ),
node.aabbMax = fmaxf( node.aabbMax, leafTri.vertex0 ),
node.aabbMax = fmaxf( node.aabbMax, leafTri.vertex1 ),
node.aabbMax = fmaxf( node.aabbMax, leafTri.vertex2 );
}
}The full Subdivide function, of which we have seen bits and pieces so far, in its full glory:
void Subdivide( uint nodeIdx )
{
// terminate recursion
BVHNode& node = bvhNode[nodeIdx];
if (node.triCount <= 2) return;
// determine split axis and position
float3 extent = node.aabbMax - node.aabbMin;
int axis = 0;
if (extent.y > extent.x) axis = 1;
if (extent.z > extent[axis]) axis = 2;
float splitPos = node.aabbMin[axis] + extent[axis] * 0.5f;
// in-place partition
int i = node.firstTriIdx;
int j = i + node.triCount - 1;
while (i <= j)
{
if (tri[triIdx[i]].centroid[axis] < splitPos)
i++;
else
swap( triIdx[i], triIdx[j--] );
}
// abort split if one of the sides is empty
int leftCount = i - node.firstTriIdx;
if (leftCount == 0 || leftCount == node.triCount) return;
// create child nodes
int leftChildIdx = nodesUsed++;
int rightChildIdx = nodesUsed++;
node.leftNode = leftChildIdx;
bvhNode[leftChildIdx].firstTriIdx = node.firstTriIdx;
bvhNode[leftChildIdx].triCount = leftCount;
bvhNode[rightChildIdx].firstTriIdx = i;
bvhNode[rightChildIdx].triCount = node.triCount - leftCount;
node.triCount = 0;
UpdateNodeBounds( leftChildIdx );
UpdateNodeBounds( rightChildIdx );
// recurse
Subdivide( leftChildIdx );
Subdivide( rightChildIdx );
}And there you have it: one valid BVH constructed from a polygon soup, in a (perhaps) surprisingly short snippet of code.
Traverse
Time to put the BVH to work. Traversing it is of course a recursive process, starting at the root node:
- Terminate if the ray misses the AABB of this node.
- If the node is a leaf: intersect the ray with the triangles in the leaf.
- Otherwise: recurse into the left and right child.
That doesn’t sound too complex, and indeed: it is implemented in just a few lines of code.
void IntersectBVH( Ray& ray, const uint nodeIdx )
{
BVHNode& node = bvhNode[nodeIdx];
if (!IntersectAABB( ray, node.aabbMin, node.aabbMax )) return;
if (node.isLeaf())
{
for (uint i = 0; i < node.triCount; i++ )
IntersectTri( ray, tri[node.firstPrim + i] );
}
else
{
IntersectBVH( ray, node.leftNode );
IntersectBVH( ray, node.leftNode + 1 );
}
}The IntersectAABB function is one function we did not implement yet. To detect if a ray intersects an AABB we use the slab test. Note that we don’t care where we hit the box; the only info we need is a yes/no answer. Without further explanation:
bool IntersectAABB( const Ray& ray, const float3 bmin, const float3 bmax )
{
float tx1 = (bmin.x - ray.O.x) / ray.D.x, tx2 = (bmax.x - ray.O.x) / ray.D.x;
float tmin = min( tx1, tx2 ), tmax = max( tx1, tx2 );
float ty1 = (bmin.y - ray.O.y) / ray.D.y, ty2 = (bmax.y - ray.O.y) / ray.D.y;
tmin = max( tmin, min( ty1, ty2 ) ), tmax = min( tmax, max( ty1, ty2 ) );
float tz1 = (bmin.z - ray.O.z) / ray.D.z, tz2 = (bmax.z - ray.O.z) / ray.D.z;
tmin = max( tmin, min( tz1, tz2 ) ), tmax = min( tmax, max( tz1, tz2 ) );
return tmax >= tmin && tmin < ray.t && tmax > 0;
}The IntersectBVH function now does the work we previously did with the loop over all the triangles. That means that this loop now simply gets replaced by a single function call:
#if 0
for( int i = 0; i < N; i++ ) IntersectTri( ray, tri[i] );
#else
IntersectBVH( ray, rootNodeIdx );
#endifQuestion is: is it any faster?
Well, on my machine I got 140 milliseconds for brute-force intersecting 64 triangles. With the BVH, this drops to (drumroll…) 32 milliseconds; a 4.4x speedup. Things get more interesting at 1024 triangles. At this scene size, frame time without BVH is 2250 milliseconds; with BVH this drops to 112 milliseconds. That is 20x faster. For larger scenes, the brute force approach becomes infeasible. And we’re only getting started: better BVHs will yield faster rays.
Dangling Pointers
In this article I postponed a lot of things. For instance: how can we make the BVHNode structure even smaller, and why should we do this? And what about the ‘ideal’ split plane axis and position? How do we safely terminate recursion in Subdivide? And what about multithreading construction?
Most of these topics are for another day, but let’s end this article with a better BVHNode structure. We currently have:
struct BVHNode
{
float3 aabbMin, aabbMax;
uint leftNode, firstTriIdx, triCount;
};This takes 36 bytes. That means that, on a modern GPU, one node fits in a 64-byte cache line, but quite frequently a node will in fact be partially in one cache line and partially in the next. This is a pretty severe performance issue. If we can reduce the BVHNode to 32 bytes, and if we align the array of nodes that we pre-allocate to a 64-byte boundary in memory (e.g. using _aligned_malloc), then every node always uses exactly half of a cache line. Even better: if we are careful, the two children of a node will be in the same cache line (for the inpatient: skip one node after the root to achieve this).
We can reach the 32-byte node size when we realize that a node that has triangles must be a leaf. It thus has no child nodes. And the other way round: if there are child nodes, there are no triangles. We thus need to store a child node index or the index of the first triangle. That means these can be stored in one and the same variable:
struct BVHNode
{
float3 aabbMin, aabbMax;
uint leftFirst, triCount;
};How we interpret this mysterious ‘leftFirst’ variable depends on triCount. If it is 0, leftFirst contains the index of the left child node. Otherwise, it contains the index of the first triangle index.
There you have it: 32 bytes for one BVH node. It doesn’t get any better. Or perhaps it does. We’ll see, in a later article.
Closing Remarks
The complete code for this project (for Windows / Visual Studio) can be found on GitHub.
Enjoyed the article? Spotted an error?
Ping me on Twitter (@j_bikker), comment on this article, or send an email to bikker.j@gmail.com.
You can also find me on Github: https://github.com/jbikker.
Or read some more articles: https://jacco.ompf2.com. Some favorites:
from Hacker News https://ift.tt/jdEtoaA
No comments:
Post a Comment
Note: Only a member of this blog may post a comment.