Has the Lead-Crime Hypothesis Been Debunked?

A couple of months ago a new paper was released that examined the lead-crime hypothesis. Its conclusion is that there's little evidence for an association, and if there is one it's pretty small.

I haven't commented on it, but not because of its negative conclusion. It's because the paper is a meta-analysis. I'm fairly proficient at plowing through papers that look at specific examples of lead and crime, but a meta-analysis is a different beast altogether: It rounds up all the papers on a particular subject and tries to estimate the average result among them. This is a specialized enterprise, which means I don't have the econometric chops to evaluate this paper. I've basically been waiting for comments from someone else in the lead-crime community who is qualified to judge it.

That hasn't happened yet, and I keep getting asked about it. So, with the caveat that I can't evaluate the methodology of this paper at the proper level, here's what it's all about. I'll add some comments and criticisms of my own, but keep in mind that they're extremely tentative.

The goal of the authors is to look at every paper they can find that draws quantitative conclusions about the lead-crime hypothesis. Then they take the results and normalize them so they can all be compared to each other on a common scale. Here's their final set of 24 papers:

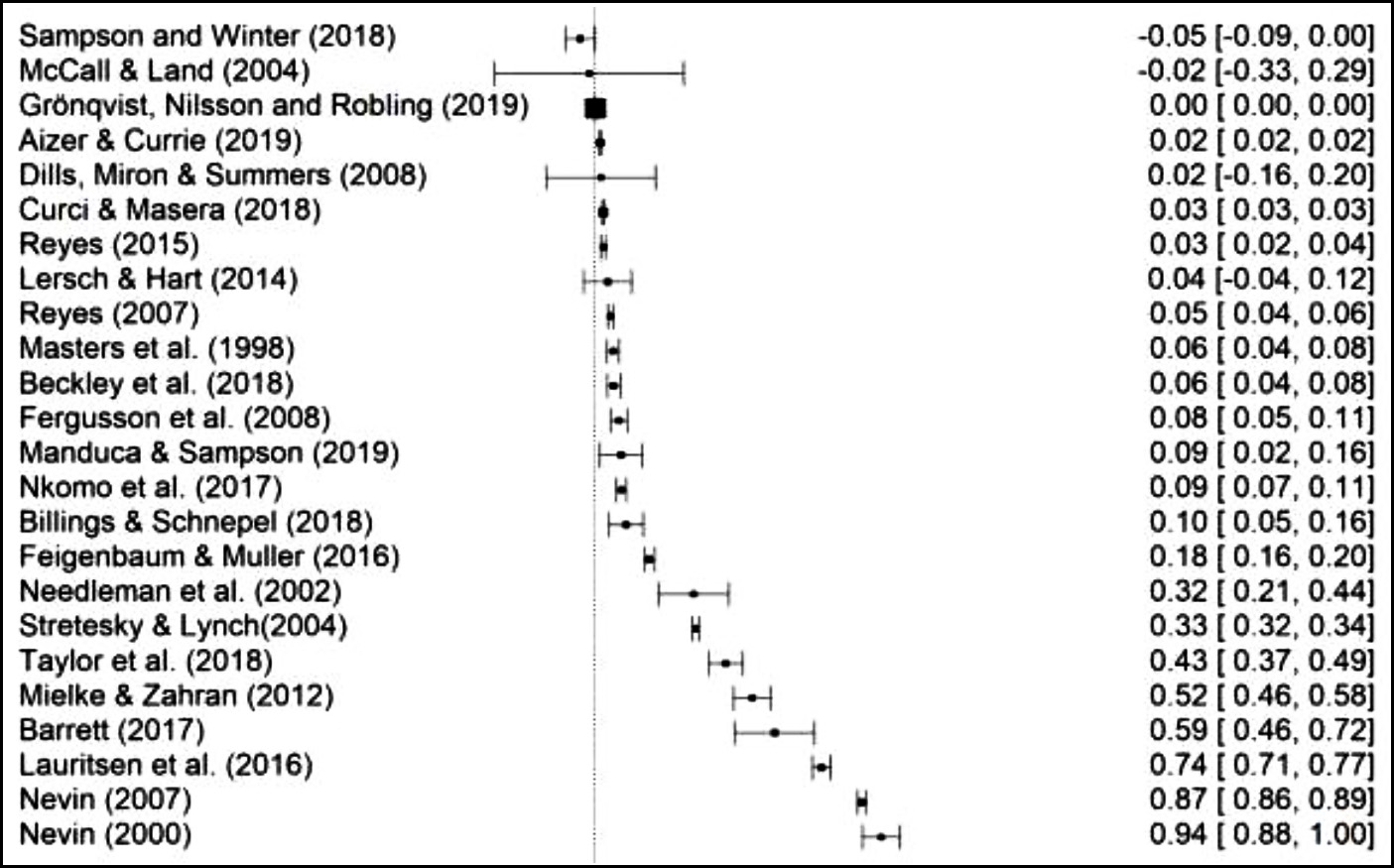
The first thing I'd note is that I'd probably discard anything prior to 2005 or so, even though that would eliminate the original 2000 paper by Rick Nevin that started the whole thing. Aside from some very rough correlations, there just wasn't enough evidence before then to draw any serious conclusions.

I also note that they left out a good paper by Brian Boutwell, but that may just be one of the seven papers they discarded because the results couldn't be normalized in a way that allowed them to be used. This is a common issue with meta-analyses, and there's not much to be done about it. Still, it does mean that high-quality studies often get discarded for arbitrary reasons.

But none of this is really the core of the meta-analysis. In fact, you might notice that among post-2005 studies, there's only one that shows a negative effect (a smallish study that found a large effect on juvenile behavior but no effect on arrest rates) and one other that showed zero effect (which is odd, since I recall that it did show a positive effect, something confirmed by the abstract). This means that 22 out of 24 studies found positive associations. Not bad! So what's the problem?

The problem is precisely that so many of the studies showed positive results. The authors present a model that says there should be more papers showing negative effects just by chance. They conclude that the reason they can't find any is due to the well-known (and very real) problem of publication bias: namely that papers with null results are boring and often never get published (or maybe never even get written up and submitted in the first place). After the authors use their model to estimate how many unpublished papers probably exist, they conclude that the average effect of lead on crime is likely zero.¹

With the caveat, yet again, that this is beyond my expertise, I don't get this. If, say, the actual effect of lead on crime is 0.33 on their scale (a "large" effect size) then you'd expect to find papers clustered around that value. Since zero is a long way away, you wouldn't expect very many studies that showed zero association or less.²

So that's one question. The authors also state that homicide rates provide the best data for studies of lead and crime, which presumably gives homicide studies extra weight in their analysis of "high-quality" studies. In fact, because the sample size for homicides is so small, exactly the opposite is true. In general, studies that look at homicide rates in the '80s and '90s simply don't have the power to be meaningful. The unit of study should always be an index value for violent crime and it should always be over a significant period of time.

And there's another thing. These crime studies aren't like drug efficacy studies, where pharma companies have an incentive to bury negative results. Nor are they the kind of study where you round up a hundred undergraduates and perform an experiment on them. A simple thing like that is just not worth writing up if it shows no effect.

On the contrary, studies of lead and crime are typically very serious pieces of research that make use of large datasets and often take years to complete. It's possible that such a study couldn't find a home if it showed no effect, but I'm not sure I buy it. Lead and crime is a fairly hot topic these days with plenty of doubters still around. Well-done papers showing no effect would probably be welcomed.

For what it's worth, I'd also note that the lead-crime field is compact enough that practitioners are typically aware of research and working papers currently in progress. They'd notice if lots of studies they knew about just disappeared for some reason. And maybe they have! But if so, they're keeping mighty quiet about it. Someone should ask them.

I have a few other questions about this meta-analysis, but they aren't important. The primary question is pretty simple: Is the lack of negative results due to papers not getting published for one reason or another? Or is it the result of lead having a substantial effect, which makes it very unlikely for a study to show an association less than zero just by chance?

And this is where I have to stop. I can bring up questions about this meta-analysis, but the authors' model is too complex for me to assess. I also don't have enough background in the meta-analysis biz to judge the paper as a whole. Someone else will have to do it, and it will have to be someone who is (a) familiar with the lead-crime field and (b) has the mathematical chops to dive into this. Any volunteers?

¹The paper shows a spike of results right around zero that's not symmetrical. That is, there's a clump of results just above zero and not very many just below. They conclude that this suggests publication bias, which is possible. But it might also just be an example p-hacking, where researchers putter around in their data until they can nudge it just above zero. This is also a known problem, but it would have only a small effect on the reported effect of lead on crime.

²As it happens, the paper doesn't show this. There's a kinda sorta spike around 0.33, but only if you squint. For the most part, there's just a smooth array of results from 0 to 1. If this is accurate, it is a bit odd, but hardly inexplicable since every study of lead and crime is working with entirely different datasets.

POSTSCRIPT: One unrelated issue that the paper raises is that violent crime in Europe generally rose in the 1990s and aughts, even as gasoline lead decreased. I've read specific papers about Sweden, Australia, and New Zealand that support the lead-crime hypothesis, all of which showed crime declines as lead levels dropped. I also know that violent crime in the UK shows an almost perfect correlation with lead levels as violent crime rose and fell. And of course Rick Nevin has shown good correlations in a number of countries.

This is just off the top of my head, and I don't know the overall data well enough to comment any further—though keep in mind that Europe generally banned leaded gasoline well after the US, so their violent crime rate kept increasing long after the US too. In any case, maybe I'll look into it. If it turned out that most European countries showed little correlation between lead levels in children and violent crime rates later in life, it would be a serious setback to the lead-crime hypothesis.

from Hacker News https://ift.tt/3uEn1Lq